Наивный байесовский классификатор

Идея: Используем теорему Байеса для классификации

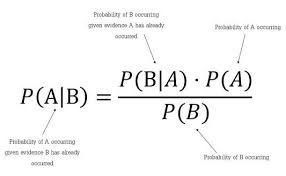
Теорема Байеса:

P(A|B) = P(B|A) × P(A) / P(B)

В нашем случае:

P(класс|признаки) = P(признаки|класс) × P(класс) / P(признаки)

Где:
- P(класс|признаки) — вероятность класса при заданных признаках (что нам нужно)
- P(признаки|класс) — вероятность признаков при данном классе
- P(класс) — априорная вероятность класса
- P(признаки) — вероятность признаков (константа для сравнения)

---

"Наивное" предположение

Ключевое упрощение: признаки независимы при условии класса

P(признаки|класс) = P(x₁|класс) × P(x₂|класс) × ... × P(xₙ|класс)

Почему "наивное"? В реальности признаки часто коррелируют, но модель всё равно работает удивительно хорошо!

---

Разбор на конкретном примере

Датасет: Определяем, идти ли на прогулку

Погода	Ветер	Температура	Идти? (класс)
Солнечно	Слабый	Тепло	Да
Солнечно	Сильный	Тепло	Да
Солнечно	Слабый	Холодно	Да
Дождь	Слабый	Тепло	Нет
Дождь	Сильный	Холодно	Нет
Облачно	Слабый	Тепло	Да
Облачно	Сильный	Тепло	Нет

Задача: Предсказать, идти ли на прогулку при:
- Погода = Солнечно
- Ветер = Слабый
- Температура = Холодно

---

Шаг 1: Считаем априорные вероятности классов

Всего 7 примеров:
- "Да" (идти): 4 раза
- "Нет" (не идти): 3 раза

P(Да) = 4/7 ≈ 0.571
P(Нет) = 3/7 ≈ 0.429

---

Шаг 2: Считаем условные вероятности для "Да"

Для класса "Да" (4 примера):

1. Погода = "Солнечно" при классе "Да":
- Примеры с "Да": [Солнечно,Слабый,Тепло], [Солнечно,Сильный,Тепло], [Солнечно,Слабый,Холодно], [Облачно,Слабый,Тепло]
- Из них "Солнечно": 3 раза

P(Погода=Солнечно|Да) = 3/4 = 0.75

2. Ветер = "Слабый" при классе "Да":
- Примеры с "Да": их 4
- Из них "Слабый": 3 раза ([Солнечно,Слабый,Тепло], [Солнечно,Слабый,Холодно], [Облачно,Слабый,Тепло])

P(Ветер=Слабый|Да) = 3/4 = 0.75

3. Температура = "Холодно" при классе "Да":
- Примеры с "Да": их 4
- Из них "Холодно": 1 раз ([Солнечно,Слабый,Холодно])

P(Температура=Холодно|Да) = 1/4 = 0.25

---

Шаг 3: Считаем условные вероятности для "Нет"

Для класса "Нет" (3 примера):

1. Погода = "Солнечно" при классе "Нет":
- Примеры с "Нет": [Дождь,Слабый,Тепло], [Дождь,Сильный,Холодно], [Облачно,Сильный,Тепло]
- Из них "Солнечно": 0 раз

P(Погода=Солнечно|Нет) = 0/3 = 0

Проблема: Нулевая вероятность! Решение — сглаживание Лапласа.

---

Шаг 4: Применяем сглаживание Лапласа

Добавляем 1 к числителю и k к знаменателю, где k — число возможных значений признака.

Для Погоды: значения = {Солнечно, Дождь, Облачно} → k=3

P(Погода=Солнечно|Нет) = (0 + 1) / (3 + 3) = 1/6 ≈ 0.167

Для остальных признаков (класс "Нет"):

P(Ветер=Слабый|Нет) = (1 + 1) / (3 + 2) = 2/5 = 0.4
(Было: "Слабый" встречался 1 раз в [Дождь,Слабый,Тепло])

P(Температура=Холодно|Нет) = (1 + 1) / (3 + 2) = 2/5 = 0.4  
(Было: "Холодно" встречался 1 раз в [Дождь,Сильный,Холодно])

---

Шаг 5: Предсказание для нового объекта

Объект: Погода=Солнечно, Ветер=Слабый, Температура=Холодно

Вычисляем для класса "Да":

P(Да|признаки) ∼ P(Да) × P(Солнечно|Да) × P(Слабый|Да) × P(Холодно|Да)
              ∼ 0.571 × 0.75 × 0.75 × 0.25
              ∼ 0.571 × 0.140625
              ∼ 0.080

Вычисляем для класса "Нет":

P(Нет|признаки) ∼ P(Нет) × P(Солнечно|Нет) × P(Слабый|Нет) × P(Холодно|Нет)
               ∼ 0.429 × 0.167 × 0.4 × 0.4
               ∼ 0.429 × 0.02672
               ∼ 0.0115

---

Шаг 6: Нормализация

Сумма "ненастоящих" вероятностей: 0.080 + 0.0115 = 0.0915

P(Да|признаки) = 0.080 / 0.0915 ≈ 0.874 (87.4%)
P(Нет|признаки) = 0.0115 / 0.0915 ≈ 0.126 (12.6%)

Результат: Идти на прогулку с вероятностью 87.4%!

---

Почему это работает на практике?

Преимущества:

1. Очень быстрый — обучение и предсказание за O(n)
2. Хорошо работает с категориальными признаками
3. Устойчив к шуму и пропускам
4. Прозрачная логика — можно понять, почему такой прогноз

Ограничения:

1. "Наивное" предположение — признаки редко полностью независимы
2. Проблема с непрерывными признаками — нужно дискретизировать или использовать распределения
3. Чувствителен к редким комбинациям

---

Варианты для непрерывных признаков

Если признак непрерывный (например, "температура=18.5°C"):

1. Гауссовский наивный Байес:

Предполагаем, что признак имеет нормальное распределение внутри класса:

P(x|класс) = (1/√(2πσ²)) × e^(-(x-μ)²/(2σ²))

Где:
- μ — среднее значение признака для класса
- σ² — дисперсия признака для класса

2. Дискретизация:

Разбиваем на интервалы:
- Холодно: <15°C
- Тепло: 15-25°C
- Жарко: >25°C

---

Практическое применение

Где работает хорошо:

1. Спам-фильтрация — слова как признаки
2. Классификация текстов — новости, отзывы
3. Медицинская диагностика — симптомы как признаки
4. Простые классификаторы — когда важна скорость

Код на Python:

from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB

# Для категориальных признаков с частотностью
model = MultinomialNB(alpha=1.0)  # alpha - параметр сглаживания

# Для непрерывных признаков (гауссовских)
model = GaussianNB()

# Для бинарных признаков (0/1)
model = BernoulliNB()

---

Итог: Когда использовать?

Используйте Наивный Байес, когда:

• Нужна максимальная скорость
• Много признаков
• Признаки можно считать условно независимыми
• Нужен простой и интерпретируемый baseline

Не используйте, когда:

• Признаки сильно коррелируют
• Нужна максимальная точность
• Важны взаимодействия между признаками

Простота — сила! Часто даёт результаты, сравнимые с более сложными моделями, при намного меньших затратах.