DeepLearning Blog

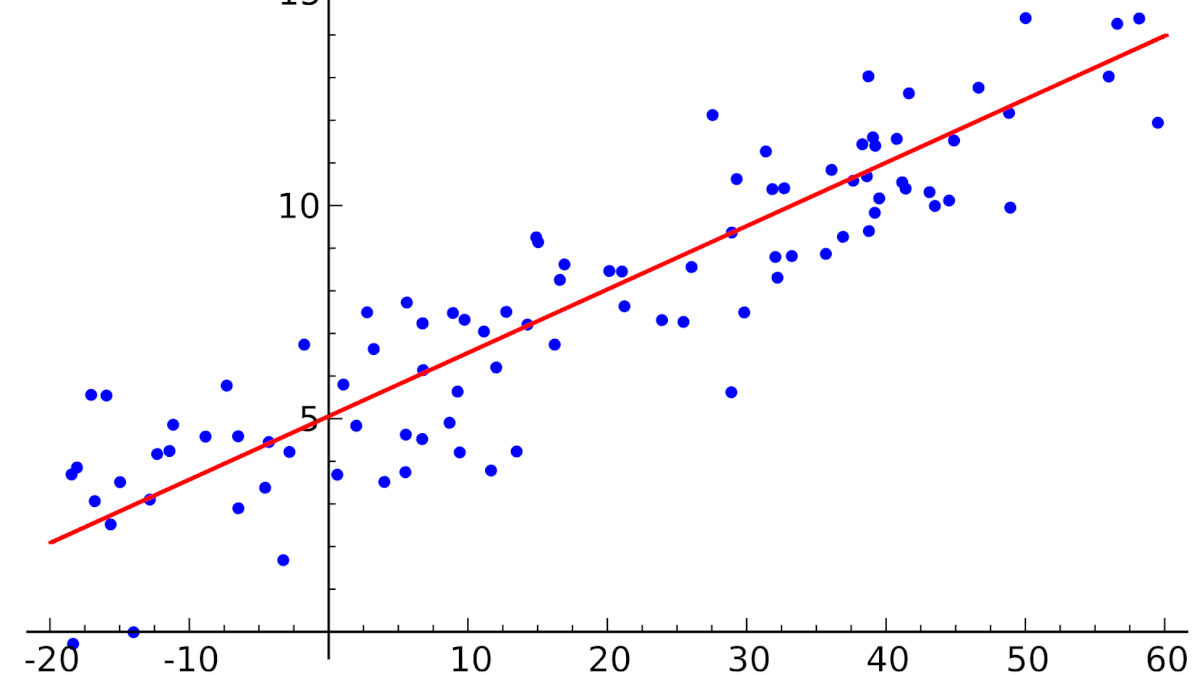
Как устроены линейные модели?

Линейные модели предсказывают целевую переменную как линейную комбинацию признаков:
- Каждому признаку присваивается свой "вес" (коэффициент)
- Предсказание = сумма (признак × вес) + свободный член
- Формула: $y = w_0 + w_1x_1 + w_2x_2 + ... + w_mx_m$

Чем линейная регрессия отличается от логистической?

Критерий	Линейная регрессия	Логистическая регрессия
Тип задачи	Регрессия (предсказание числа)	Классификация (бинарная/мультикласс)
Выход	Любое число	Вероятность от 0 до 1
Актуально для	Цены, температура, время	Спам/не спам, болен/здоров
Функция	Прямая зависимость	Сигмоида: $p = 1 / (1 + e^{-z})$

Простыми словами: Линейная регрессия предсказывает "сколько", логистическая — "к какому классу относится".

Плюсы и минусы линейных моделей

✅ Плюсы:

1. Простота и скорость — быстро обучаются, мало вычислений
2. Интерпретируемость — можно понять вклад каждого признака
3. Надёжность — меньше склонны к переобучению
4. Хороший baseline — всегда стоит попробовать сначала

❌ Минусы:

1. Предполагают линейность — не работают на сложных нелинейных данных
2. Чувствительны к выбросам — один выброс может сильно всё испортить
3. Требуют подготовки — нужно масштабировать признаки
4. Проблемы с мультиколлинеарностью — если признаки коррелируют
   
   

Что такое мультиколлинеарность и как с ней бороться?

Мультиколлинеарность — когда признаки сильно связаны между собой.

Пример: В модели есть "рост в см" и "рост в дюймах" — это по сути один и тот же признак!

Проблемы:

• Веса становятся нестабильными
• Сложно интерпретировать вклад каждого признака
• Модель может работать плохо

Как бороться:

1. Удалить лишние признаки — оставить только один из коррелирующих
2. Объединить признаки — создать один общий признак
3. Использовать PCA — преобразовать в независимые компоненты
4. Применить регуляризацию — специально "наказать" модель за сложность
   
   

Что такое регуляризация?

Регуляризация — это техника, которая не даёт модели стать слишком сложной.

Аналогия: Если ребёнку дать слишком много свободы (большие веса в модели), он начнёт запоминать шум (переобучаться). Регуляризация — как разумные ограничения.

Как работает: К обычной функции ошибки добавляется "штраф" за большие веса:
- Общая ошибка = Ошибка предсказания + Штраф за сложность
- Формула: $Loss_{new} = Loss_{old} + λ × R(w)$

Зачем нужно: Помогает бороться с переобучением, особенно когда много признаков.

Виды регуляризации: L1, L2, Elastic Net

1. L2-регуляризация (Ridge)

• Штраф: Сумма квадратов весов
• Эффект: Уменьшает все веса, но не до нуля
• Плюс: Устойчива, хорошо работает при корреляции признаков
• Минус: Все признаки остаются в модели
  
  

2. L1-регуляризация (Lasso)

• Штраф: Сумма модулей весов
• Эффект: Некоторые веса становятся РОВНО НУЛЬ
• Плюс: Автоматический отбор признаков!
• Минус: Менее устойчива при корреляции признаков
  
  

3. Elastic Net

• Комбинация L1 и L2
• Формула: $α × L1 + (1-α) × L2$
• Плюсы: Сочетает преимущества обоих методов
• Когда использовать: Когда много признаков и они коррелируют

---

Когда что использовать?

Ситуация	Что выбрать
Все признаки важны, нужно уменьшить переобучение	L2 (Ridge)
Много признаков, нужен отбор самых важных	L1 (Lasso)
Признаки коррелируют, но нужен отбор	Elastic Net
Мало данных, нужно максимальная интерпретируемость	Без регуляризации

Простое правило: Начинайте с Ridge, если нужно отбирать признаки — переходите на Lasso или Elastic Net.